Введение

Поиск, вставка и удаление, как известно, – основные операции при работе с данными. Мы начнем с исследования того, как эти операции реализуются над самыми известными объектами – массивами и (связанными) списками. Предполагается, что с каждым элементом, помимо собственно информационной его части, сопоставлен еще ключ, значения которого и используются для принятия решения о судьбе элемента. Полагаю, нет нужды говорить о том, что ключ может быть одним из полей информационной части элемента.

Массивы

На рис.1.1 показан массив из семи элементов с числовыми значениями. Чтобы найти в нем нужное нам число, мы можем использовать линейный поиск – его алгоритм приведен на рис. 1.2. Максимальное число сравнений при таком поиске – 7; оно достигается в случае, когда нужное нам значение находится в элементе A[6].

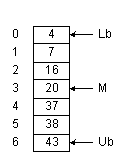
Рис. 1.1. Массивы

Если известно, что данные отсортированы, можно применить двоичный поиск (рис. 1.3). Переменные Lb и Ub содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Мы начинаем всегда с исследования среднего элемента отрезка. Если искомое значение меньше среднего элемента, мы переходим к поиску в верхней половине отрезка, где все элементы меньше только что проверенного. Другими словами, значением Ub становится (M – 1) и на следующей итерации мы работаем с половиной массива. Таким образом, в результате каждой проверки мы вдвое сужаем область поиска. Так, в нашем примере, после первой итерации область поиска – всего лишь три элемента, после второй остается всего лишь один элемент. Таким образом, если длина массива равна 6, нам достаточно трех итераций, чтобы найти нужное число.

Двоичный поиск - очень мощный метод. Если, например, длина массива равна 1023, после первого сравнения область сужается до 511 элементов, а после второй - до 255. Легко посчитать, что для поиска в массиве из 1023 элементов достаточно 10 сравнений.

Кроме поиска нам бывает нужно вставлять и удалять элементы. К сожалению, массив плохо приспособлен для выполнения этих операций. Например, чтобы вставить число 18 в массив на рис. 1.1, нам понадобится сдвинуть элементы A[3]:A[6] вниз - лишь после этого мы сможем записать число 18 в элемент A[3]. Аналогичная проблема возникает при удалении элементов. Для повышения эффективности операций вставки/удаления предложены связанные списки.

int function BinarySearch (Array A, int Lb, int Ub, int Key); begin   do forever     M = (Lb + Ub)/2;     if (Key < A[M]) then       Ub = M - 1;     else if (Key > A[M]) then       Lb = M + 1;     else       return M;     if (Lb > Ub) then     return -1; end;

Рис. 1.3. Двоичный поиск

Односвязные списки

На рис. 1.4 те же числа, что и раньше, хранятся в виде связанного списка; слово "связанный" часто опускают. Предполагая, что X и P являются указателями, число 18 можно вставить в такой список следующим образом:

X->Next = P->Next;

P->Next = X;

Списки позволяют очень эффективно вставлять и удалять. Поинтересуемся, однако, как найти место, куда мы будем вставлять новый элемент, т.е. каким образом присвоить нужное значение указателю P. Увы, для поиска нужной точки придется прогуляться по элементам списка. Таким образом, переход к спискам позволяет уменьшить время вставки/удаления элемента, однако операция поиска требует больше времени за счет последовательного доступа к элементам списка. –Этот недостаток устранен в бинарных деревьях, ориентированных как раз на эффективный двоичный поиск.

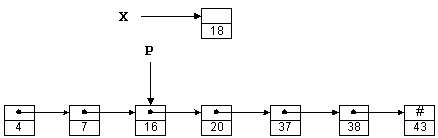
Рис. 1.4. Односвязный список

Оценки времени исполнения

Для оценки производительности алгоритмов можно использовать разные подходы. Самый бесхитростный - просто запустить каждый алгоритм на нескольких задачах и сравнить время исполнения. Другой способ - оценить время исполнения. Например, мы можем утверждать, что время поиска есть O(n) (читается так: «о большое от n»). Это означает, что при больших n время поиска не сильно больше, чем количество элементов. Когда используют обозначение O(), имеют в виду не точное время исполнения, а только его предел сверху, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n²), имеют в виду, что время исполнения задачи растет не быстрее, чем некоторая константа, помноженная на квадрат количества элементов. Чтобы почувствовать, что это такое, посмотрите таблицу 1.1, где приведены числа, иллюстрирующие скорость роста для нескольких разных функций. Скорость роста O(lg n) характеризует алгоритмы типа двоичного поиска. Логарифм по основанию 2 увеличивается на 1, когда n удваивается. Вспомните - каждое новое сравнение позволяет нам искать в вдвое меньшем списке. Именно поэтому говорят, что время работы при двоичном поиске растет как lg n.

Таблица 1.1. Скорость роста нескольких функций

Если считать, что числа в таблице 1.1 соответствуют микросекундам, то для задачи с 1048476 элементами алгоритму с временем работы O(lg n) потребуется 20 микросекунд, алгоритму с временем работы O(n^1.25) - порядка 33 секунд, алгоритму с временем работы O(n²) - более 12 дней. В нижеследующем тексте для каждого алгоритма приведены соответствующие O-оценки. Более точные формулировки и доказательства можно найти в приводимых литературных ссылках.

Итак...

Как мы видели, если массив отсортирован, то искать его элементы нужно с помощью двоичного поиска. Однако, не забудем, кто-то должен отсортировать наш массив! В следующем разделе мы исследуем разные способы сортировки массива. Оказывается, эта задача встречается достаточно часто и требует заметных вычислительных ресурсов, поэтому сортирующие алгоритмы исследованы вдоль и поперек, известны алгоритмы, эффективность которых достигла теоретического предела.

Связанные списки позволяют эффективно вставлять и удалять элементы, но поиск в них последователен и потому отнимает много времени. Имеются алгоритмы, позволяющие эффективно выполнять все три операции, мы обсудим из в разделе о словарях.

<DIV ALIGN=right></DIV>

Сортировка

Здесь представлены несколько алгоритмов, в том числе - сортировка вставками, метод Шелла и быстрый поиск (более известный под исходным, английским, именем QuickSort). Сортировка вставками - простейший метод, который, к тому же, не требует дополнительной памяти. Метод Шелла - простая модификация сортировки вставками, которая радикально отличается от нее производительностью. По-видимому, наиболее эффективный и популярный метод - QuickSort, только он применим при сортировке больших массивов.

Сортировка вставками

Один из простейших способов отсортировать массив - сортировка вставками. В обычной жизни мы сталкиваемся с этим методом при игре в карты. Чтобы отсортировать имеющиеся у вас карты, вы вынимаете карту, сдвигаете оставшиеся карты, а затем вставляете карту на нужное место. Процесс повторяется до тех пор, пока хоть одна карта не на месте. Как среднее, так и худшее время для этого алгоритма - O(n²). Дальнейшую информацию можно получить в книжке Кнута [1998]

Теория

На рис.2.1(a) мы вынимаем элемент 3. Затем элементы, расположенные выше, сдвигаем вниз - до тех пор, пока не найдем место, куда нужно вставить 3. Это процесс продолжается на рис.2.1(b) для числа 1. Наконец, на рис.2.1(c) мы завершаем сортировку, поместив 2 на нужное место.

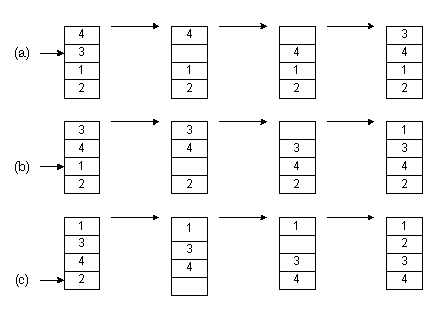
Рис. 2-1. Сортировка вставками

Если длина нашего массива равна n, нам нужно пройтись по n - 1 элементам. Каждый раз нам может понадобиться сдвинуть n - 1 других элементов, получая алгоритм с временем работы O(n²).

Сортировка вставками относится к числу методов сортировки по месту. Другими словами, ей не требуется вспомогательная память, мы сортируем элементы массива, используя только память, занимаемую самим массивом. Кроме того, она является устойчивой - если среди сортируемых ключей имеются одинаковые, после сортировки они остаются в исходном порядке.