Линейный выбор с подсчетом

Метод сортировки с подсчетом описывается в литературе как процедура упорядочения внутреннего списка чисел. Фактически, это не метод сортировки, а технический приём, который можно использовать в различных методах для сокращения количества обменов или их полного устранения. Он является формой индексирования, в которой счетчик относительной позиции каждого элемента корректируется в течение процесса сравнения. Здесь он описан применительно к линейному выбору.

Память, используемая линейным выбором с подсчетом, будет включать область вывода (также как и при линейном выборе) для хранения окончательно упорядоченного списка. Размер её отвечает тем же соображениям, что и при линейном выборе. Дополнительно должна быть обеспечена память под счетчик для каждого элемента списка. В результате действий над значениями этих счетчиков образуется множество индексов позиций для элементов в упорядоченном списке. При каждом просмотре ключ сравнивается со своими линейными преемниками. Каждый раз, когда находится больший ключ, его счетчик увеличивается на единицу. Если найденный ключ меньше или равен, то увеличивается счетчик, соответствующий большему из сравниваемых ключей. Следовательно, в любой момент времени счетчик элемента указывает количество ключей, о которых известно, что они меньше ключа рассматриваемого элемента. При первом просмотре первый ключ в списке сравнивается со всеми остальными ключами. В его счетчике подсчитывается количество меньших ключей. В счетчиках больших ключей будут 1. При втором просмотре первый ключ не рассматривается. Второй ключ сравнивается с ключами всех преемников. Подсчеты фиксируются. Этот процесс продолжается N-1 раз. На этом этапе известна относительная позиция каждого элемента. Помещая ключи в выходной список в соответствии со значениями их счетчиков, получаем упорядоченный список.

Реализация

procedure ViborSPodschetom;

  var

   i,j:index;

   count: array [index] of integer;

   B: array [index] of item;

  begin

   for i:=1 to n do count[i]:=0;

    for i:=1 to n-1 do

      begin

       for j:=i+1 to n do

        begin

         if (A[i].key<A[j].key) then count[j]:=count[j]+1 else count[i]:=count[i]+1;

        end;

      end;

   for i:=1 to n do B[count[i]+1]:=A[i];

   for i:=1 to n do A[i]:=B[i];

  end;

Сортировка обменом

Парный обмен

Метод парного обмена(также называемый "нечётно-чётная перестановка”) состоит из различного числа "нечётных” и "чётных” просмотров. При нечётных просмотрах каждый элемент из нечетной позиции сравнивается со своим соседом из чётной позиции и больший из них занимает четную позицию. Нисходящий просмотр списка продолжается до тех пор, пока последний нечетный (N-1) не сравнивается с последним четным элементом (N). Если нечетное число элементов, то последний элемент не будет участвовать в сравнении. В течение каждого просмотра ведется подсчет обменов.

При четных просмотрах четные позиции сравниваются с соседними нечетными. Обмены выполняются тогда, когда надо, чтобы больший из пары занял нечетную позицию. Таким образом, ключи с большими значениями перемещаются на дно списка. При этом должно быть столько просмотров, сколько необходимо для того, чтобы переместить в позицию число, наиболее удаленное от своей конечной позиции. Затем выполняется заключительный просмотр, необходимый для того, чтобы опознать упорядоченность. В течение этого просмотра счетчик обменов равен 0. Данный метод требует по крайней мере двух просмотров – одного нечётного и одного чётного.

Парный обмен, просмотры

Начальные ключи.   i=2    3     4     5    6    7    8

              67    67    67    94    94   94   94   94

Реализация

procedure ParnajaSort;

  var

   i:index;

   x:item;

   nechet:boolean;

   obmen,j:integer;

  begin

    nechet:=true; j:=0;

    repeat

     obmen:=0;

     if nechet then i:=1 else i:=2;

       repeat

         if (A[i].key > A[i+1].key) then

              begin

                x:=A[i]; A[i]:=A[i+1]; A[i+1]:=x;

                obmen:=obmen+1;

              end;

        i:=i+2;

       until (i>=n);

       j:=j+1;

       if nechet=true then nechet:=false else nechet:=true;

    until(obmen=0) and (j>=2);

   end;

Стандартный обмен

Классификация методов сортировки не всегда четко определена. Оба представленных ранее метода можно рассматривать как сортировку обменом. Однако в этом разделе мы остановимся на методе, в котором обмен двух элементов является основной характеристикой процесса. Приведенный ниже алгоритм сортировки простым обменом основан на принципе сравнения и обмена пары соседних элементов до тех пор, пока не будут рассортированы все элементы.

Как и в предыдущих методах простого выбора, мы совершаем повторные проходы по массиву, каждый раз просеивая наименьший элемент оставшегося множества,  двигаясь к левому концу массива. Если для разнообразия мы будем рассматривать массив, расположенный вертикально, а не горизонтально, и представим себе элементы пузырьками в резервуаре с водой, обладающими «весами» соответствующих их ключам,  то каждый проход по массиву будет приводить к «всплыванию» пузырька на уровень соответствующий его «весу».

Начальные ключи.   i=2    3     4     5    6    7    8

              67    67    67    94    94   94   94   94

Этот метод широко известен как сортировка методом пузырька. Его простейший вариант приведен в программе ниже.

    procedure BubbleSort;

      var i,j: index; x: item;

    begin for i:= 2 to n do

        begin for j:= n downto i do

         if (A[j-1].key > A[j].key) then

         begin x:=A[j-1]; A[j-1]:=A[j]; A[j]:=x;

         end;

       end;

   end; {BubbleSort}

Шейкер-сортировка

Этот предыдущий алгоритм легко оптимизировать. Пример показывает, что три последних прохода никак не влияют на порядок элементов, поскольку те уже рассортированы. Очевидный способ улучшить данный алгоритм – это запомнить, производится ли на данном проходе какой - либо обмен. Если нет, то это означает, что алгоритм может закончить работу. Этот процесс улучшения можно продолжить, если запомнить не только сам факт обмена, но и место (индекс) последнего обмена. Ведь ясно, что все пары соседних элементов с  индексами меньшими этого индекса k, уже расположены в нужном порядке. Поэтому следующие проходы можно заканчивать на этом индексе вместо того чтобы двигаться до установленной заранее нижней границы i. Однако внимательный программист заметит здесь странную асимметрию: один неправильно расположенный «пузырек» в тяжелом конце рассортированного массива всплывет на место за один проход, а неправильно расположенный элемент легкого конца будет опускаться на правильное место только на один шаг на каждом проходе. Например, массив 12,18,42,44,55,67,94 06 будет рассортирован при помощи метода пузырька за один проход, а сортировка массива 94,06,12,18,42,44,55,67 потребует семи проходов. Эта неестественная асимметрия подсказывает нам третье улучшение: менять направление следующих один за другим проходов. Мы назовем полученный в результате алгоритм шейкер-сортировкой. Его работа показана ниже на тех же восьми ключах, использованных в предыдущей таблице.

Программа шейкер-сортировки приведена ниже.

Реализация

    procedure ShakeSort;

      var j,k,l,r: index; x: item;

    begin l:=2; r:=n; k:=n;

     repeat

      for j:=r downto l do

        if (A[j-1].key > A[j].key) then

          begin x:=A[j-1]; A[j-1]:=A[j]; A[j]:=x;

           k:=j;

          end;

      l:=k+1;

      for j:=l to r do

        if (A[j-1].key > A[j].key) then

          begin x:=A[j-1]; A[j-1]:=A[j]; A[j]:=x;

           k:=j;

          end;

      r:=k-1;

     until (l>r);

   end; {ShakeSort}

i =   2    3     3     4     4

     r =   8    8     7     7     4

           ^    v     ^     v     ^

          55    44    44    12    12

          67    67    94    94    94

Распределяющая сортировка

Обсуждаемый здесь алгоритм сортировки отличается от рассматривавшихся до сих пор тем, что основан не на сравнениях между именами, а на представлении имен.

Мы полагаем, что каждое из имен x₁, x₂, …, x_n имеет вид

x_i=( x_i,p,x_i,p-1,…,x_i,1)

и их нужно отсортировать в возрастающем лексикографическом порядке, т.е.

x_i=(x_i,p,x_i,p-1,…,x_i,1)<(x_j,p,x_j,p-1,…,x_j,1)=x_j

тогда и только тогда, когда для некоторого t≤p имеем x_i,l = x_j,l для l>t и x_i,t<x_j,t. Для простоты будем считать, что 0≤x_i,l<r, и поэтому имена можно рассматривать как целые, представленные по основанию r, так что каждое имя имеет p r-ичных цифр. Чтобы не было имен разной длины, более короткие имена дополняются нулями.

Цифровая распределяющая сортировка основана на наблюдении, что если имена уже отсортированы по младшим разрядам l, l-1, …, 1, то их можно полностью отсортировать, сортируя только по старшим разрядам p, p-1,…, l+1 при условии, что сортировка осуществляется таким образом, чтобы не нарушить относительный порядок имен с одинаковыми цифрами в старших разрядах. Эта идея лежит в основе механических сортировальных машин для перфокарт; для сортировки карт в полях, скажем, от 76-й до 80-й колонки, они сортируются в возрастающем порядке по 80-й колонке, потом по 79-й колонке и т.д. включая и 76-ю колонку. Каждая сортировка по колонке состоит из чтения колонки каждой карты и физического перемещения карты наверх стопки, которая отвечает цифре, пробитой в этой колонке карты. Как только все карты помещены в соответствующие стопки, стопки объединяются вместе в порядке возрастания; затем процесс повторяется для следующей колонки слева. Эта процедура проиллюстрирована на примере трехзначных чисел.

Заметим, что как к стопкам, так и к самой таблице обращаются по правилу "первым включается – первым исключается”, и поэтому лучшим способом их представления являются очереди. В частности, предположим, что с каждым ключом x_i ассоциируется поле связи LINK_i; тогда эти поля связи можно использовать для сцепления всех имен в таблице вместе во входную очередь Q. При помощи полей связи можно также сцеплять имена в очереди Q₀,Q₁,…,Q_r-1, используемые для представления стопок. После того как имена распределены по стопкам, очереди, представляющие эти стопки, связываются вместе для получения вновь таблицы Q. В результате применения алгоритма очередь Q будет содержать имена в порядке возрастания; т.е. имена будут связаны в порядке возрастания полями связи, начиная с головы очереди Q.

Алгоритм распределяющей сортировки

Использовать поля связи LINK_i,…,LINK_n для формирования x₁,…,x_n во входную очередь Q

                 while Q не пуста do  пусть X=(x_p,x_p-1,…,x₁)

For j=1 to p do                       Q_xj←X

сцепить очереди Q₀, …, Q_r-1 вместе

для формирования новой очереди Q

Сортировка Шелла

Метод, предложенный Дональдом Л. Шеллом, является неустойчивой сортировкой по месту. Эффективность метода Шелла объясняется тем, что сдвигаемые элементы быстро попадают на нужные места. Среднее время для сортировки Шелла равняется O(n^1.25), для худшего случая оценкой является O(n^1.5). Дальнейшие свойства см. в книге Кнута [1998] [Knuth].

Теория

На рис. 2.2(a) был приведен пример сортировки вставками. Мы сначала вынимали 1, затем сдвигали 3 и 5 на одну позицию вниз, после чего вставляли 1. Таким образом, нам требовались два сдвига. В следующий раз нам требовалось еще два сдвига, чтобы вставить на нужное место 2. На весь процесс нам требовалось 2 + 2 + 1 = 5 сдвигов.

На рис. 2.2(b) иллюстрируется сортировка Шелла. Мы начинаем, производя сортировку вставками с шагом 2. Сначала мы рассматриваем числа 3 и 1: извлекаем 1, сдвигаем 3 на 1 позицию с шагом 2, вставляем 1. Затем повторяем то же для чисел 5 и 2: извлекаем 2, сдвигаем вниз 5, вставляем 2. И т.д. Закончив сортировку с шагом 2, производим ее с шагом 1, т.е. выполняем обычную сортировку вставками. Всего при этом нам понадобится 1 + 1 + 1 = 3 сдвига. Таким образом, использовав вначале шаг, больший 1, мы добились меньшего числа сдвигов.

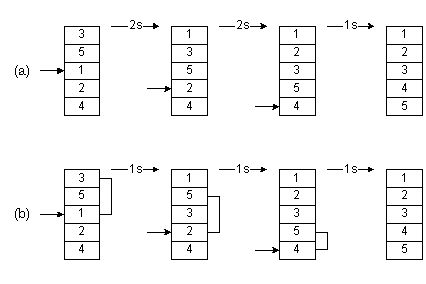
Рис. 2-2. Сортировка Шелла

Можно использовать самые разные схемы выбора шагов. Как правило, сначала мы сортируем массив с большим шагом, затем уменьшаем шаг и повторяем сортировку. В самом конце сортируем с шагом 1. Хотя этот метод легко объяснить, его формальный анализ довольно труден. В частности, теоретикам не удалось найти оптимальную схему выбора шагов. Кнут [Knuth] провел множество экспериментов и нашел следующую формулу выбора шагов h для массива длины N:

в последовательности h₁ = 1, h_s+1 = 3h_s + 1, ... взять h_t, если h_t+2 >= N.

Вот несколько первых значений h:

h₁ = 1
h₂ = (3 x 1) + 1 = 4
h₃ = (3 x 4) + 1 = 13
h₄ = (3 x 13) + 1 = 40
h₅ = (3 x 40) + 1 = 121

Чтобы отсортировать массив длиной 100, прежде всего найдем номер s, для которого h_s >= 100. Согласно приведенным цифрам, s = 5. Нужное нам значение находится двумя строчками выше. Таким образом, последовательность шагов при сортировке будет такой: 13-4-1. Ну, конечно, нам не нужно хранить эту последовательность: очередное значение h находится из предыдущего по формуле

h_s-1 = [h_s / 3].