В реализации сортировки Шелла на Си следует изменить операторы typedef T и сравнения compGT так, чтобы они соответствовали данным, хранимым в массиве. Основная часть алгоритма - сортировка вставками с шагом h.
typedef int T; /* Тип элемента, который нужно сортировать */
typedef int tblIndex; /* Тип ключа сортировки */
#define compGT(a,b) (a > b)
void shellSort(T *a, tblIndex lb, tblIndex ub) {
tblIndex n, h, i, j;
T t;
/*********************************
* сортируемый массив a[lb..ub] *
*********************************/
/* Вычисление наибольшего шага */
n = ub - lb + 1;
h = 1;
if (n < 14)
h = 1;
else if (sizeof(tblIndex) == 2 && n > 29524)
h = 3280;
else {
while (h < n) h = 3*h + 1;
h /= 3;
h /= 3;
}
while (h > 0) {
/* «Сортировка вставкой» с шагом h */
for (i = lb + h; i <= ub; i++) {
t = a[i];
for (j = i-h; j >= lb && compGT(a[j], t); j -= h)
a[j+h] = a[j];
a[j+h] = t;
}
/* Вычисление следующего шага */
h /= 3;
}
}
Хотя идея Шелла значительно улучшает сортировку вставками, резервы еще остаются. Один из наиболее известных алгоритмов сортировки - быстрая сортировка, предложенная Ч.Хоором. Метод и в самом деле очень быстр, недаром по-английски его так и величают QuickSort к неудовольствию всех «спелл-чекеров».
Этому методу требуется O(n lg n) в среднем и O(n2) в худшем случае. К
счастью, если принять адекватные предосторожности, наихудший случай крайне
маловероятен. Быстрый поиск не является устойчивым. Кроме того, ему требуется
стек, т.е. он не является и методом сортировки на месте. Дальнейшую информацию
можно получить в работе Кормена [1990] [Cormen].
Алгоритм разбивает сортируемый массив на разделы, затем рекурсивно сортирует каждый раздел. В функции Partition (рис. 2.3) один из элементов массива выбирается в качестве центрального. Ключи, меньшие центрального следует расположить слева от него, те, которые больше, - справа.
|
int function Partition (Array A, int Lb, int Ub); begin Выбрать центральный среди элементов A[Lb]...A[Ub]; Переупорядочить A[Lb]...A[Ub] так чтобы: слева от центра все значения были <= центрального справа от центра все значения были >= центрального Вернуть индекс центрального элемента; end; procedure QuickSort (Array A, int Lb, int Ub); begin if Lb < Ub then M = Partition (A, Lb, Ub); QuickSort (A, Lb, M - 1); QuickSort (A, M + 1, Ub); end; |
Рис. 2.3. Быстрый поиск
На рис. 2.4(a) в качестве центрального (pivot) выбран элемент 3. Индексы начинают изменяться с концов массива. Индекс i начинается слева и используется для выбора элементов, которые больше центрального, индекс j начинается справа и используется для выбора элементов, которые меньше центрального. Эти элементы меняются местами - см. рис. 2.4(b). Процедура QuickSort рекурсивно сортирует два подмассива, в результате получается массив, представленный на рис. 2.4(c).
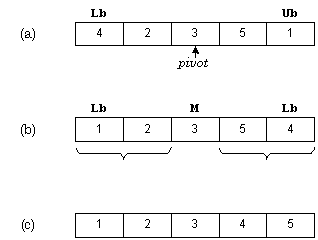
Рис 2-4. Пример работы алгоритма Quicksort
В процессе сортировки может потребоваться передвинуть центральный элемент. Если нам повезет, выбранный элемент окажется медианой значений массива, т.е. разделит его пополам. Предположим на минутку, что это и в самом деле так. Поскольку на каждом шаге мы делим массив пополам, а функция Partition в конце концов просмотрит все n элементов, время работы алгоритма есть O(n lg n).
В качестве центрального функция Partition может попросту брать первый элемент (A[Lb]). Все остальные элементы массива мы сравниваем с центральным и передвигаем либо влево от него, либо вправо. Есть, однако, один случай, который безжалостно разрушает эту прекрасную простоту. Предположим, что наш массив с самого начала отсортирован. Функция Partition всегда будет получать в качестве центрального минимальный элемент и потому разделит массив наихудшим способом: в левом разделе окажется один элемент, соответственно, в правом останется Ub - Lb элементов. Таким образом, каждый рекурсивный вызов процедуры QuickSort всего лишь уменьшит длину сортируемого массива на 1. В результате для выполнения сортировки понадобится n рекурсивных вызовов, что приводит к времени работы алгоритма порядка O(n2). Один из способов побороть эту проблему - случайно выбирать центральный элемент. Это сделает наихудший случай чрезвычайно маловероятным.
В приведенной реализации
typedef int T; /* Тип элемента, который нужно сортировать */
typedef int tblIndex; /* Тип ключа сортировки */
#define сompGT(a,b) (a > b)
tblIndex partition(T *a, tblIndex lb, tblIndex ub) {
T t, pivot;
tblIndex i, j, p;
/**********************************
* разделение массива a[lb..ub] *
**********************************/
/* выбор центрального элемента и обмен его с первым */
p = lb + ((ub - lb)>>1);
pivot = a[p];
a[p] = a[lb];
/* сортировка lb+1..ub относительно центрального элемента */
i = lb+1;
j = ub;
while (1) {
while (i < j && compGT(pivot, a[i])) i++;
while (j >= i && compGT(a[j], pivot)) j--;
if (i >= j) break;
t = a[i];
a[i] = a[j];
a[j] = t;
j--; i++;
}
/* центральный элемент размещается в a[j] */
a[lb] = a[j];
a[j] = pivot;
return j;
}
void quickSort(T *a, tblIndex lb, tblIndex ub) {
tblIndex m;
/**********************************
* сортировка массива a[lb..ub] *
**********************************/
while (lb < ub) {
/* короткие массивы сортируются методом вставки */
if (ub - lb <= 12) {
insertSort(a, lb, ub);
return;
}
/* разделение на два сегмента */
m = partition (a, lb, ub);
/* сортировка меньшего раздела */
/* требуется более короткий стек */
if (m - lb <= ub - m) {
quickSort(a, lb, m - 1);
lb = m + 1;
} else {
quickSort(a, m + 1, ub);
ub = m - 1;
}
}
}




