В реализации алгоритма на Си операторы typedef T и compGT следует изменить так, чтобы они соответствовали данным, хранимым в дереве. Каждый узел Node содержит указатели left, right на левого и правого потомков, а также указатель parent на предка. Собственно данные хранятся в поле data. Адрес узла, являющегося корнем дерева хранится в указателе root, значение которого в самом начале, естественно, NULL. Функция insertNode запрашивает память под новый узел и вставляет узел в дерево, т.е. устанавливает нужные значения нужных указателей. Функция deleteNode, напротив, удаляет узел из дерева (т.е. устанавливает нужные значения нужных указателей), а затем освобождает память, которую занимал узел. Функция findNode ищет в дереве узел, содержащий заданное значение.
typedef int T; /* type of item to be sorted */
#define compLT(a,b) (a < b)
#define compEQ(a,b) (a == b)
typedef struct Node_ {
struct Node_ *left; /* left child */
struct Node_ *right; /* right child */
struct Node_ *parent; /* parent */
T data; /* data stored in node */
} Node;
Node *root = NULL; /* root of binary tree */
Node *insertNode(T data) {
Node *x, *current, *parent;
/***********************************************
* allocate node for data and insert in tree *
***********************************************/
/* find x's parent */
current = root;
parent = 0;
while (current) {
if (compEQ(data, current->data)) return (current);
parent = current;
current = compLT(data, current->data) ?
current->left : current->right;
}
/* setup new node */
if ((x = malloc (sizeof(*x))) == 0) {
fprintf (stderr, "insufficient memory (insertNode)\n");
exit(1);
}
x->data = data;
x->parent = parent;
x->left = NULL;
x->right = NULL;
/* insert x in tree */
if(parent)
if(compLT(x->data, parent->data))
parent->left = x;
else
parent->right = x;
else
root = x;
return(x);
}
void deleteNode(Node *z) {
Node *x, *y;
/*****************************
* delete node z from tree *
*****************************/
/* y will be removed from the parent chain */
if (!z || z == NULL) return;
/* find tree successor */
if (z->left == NULL || z->right == NULL)
y = z;
else {
y = z->right;
while (y->left != NULL) y = y->left;
}
/* x is y's only child */
if (y->left != NULL)
x = y->left;
else
x = y->right;
/* remove y from the parent chain */
if (x) x->parent = y->parent;
if (y->parent)
if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
else
root = x;
/* y is the node we're removing */
/* z is the data we're removing */
/* if z and y are not the same, replace z with y. */
if (y != z) {
y->left = z->left;
if (y->left) y->left->parent = y;
y->right = z->right;
if (y->right) y->right->parent = y;
y->parent = z->parent;
if (z->parent)
if (z == z->parent->left)
z->parent->left = y;
else
z->parent->right = y;
else
root = y;
free (z);
} else {
free (y);
}
}
Node *findNode(T data) {
/*******************************
* find node containing data *
*******************************/
Node *current = root;
while(current != NULL)
if(compEQ(data, current->data))
return (current);
else
current = compLT(data, current->data) ?
current->left : current->right;
return(0);
}
<DIV ALIGN=right></DIV>
Двоичные деревья работают лучше всего, когда они сбалансированы, когда длина пути от корня до любого из листьев находится в определенных пределах, связанных с числом узлов. Красно-черные деревья - один из способов балансировки деревьев. Название происходит от стандартной раскраски узлов таких деревьев в красный и черный цвета. Цвета узлов используются при балансировке дерева. Во время операций вставки и удаления поддеревья может понадобиться повернуть, чтобы достигнуть сбалансированности дерева. Оценкой как среднего время, так и наихудшего является O(lg n).
Этот раздел - один из наиболее трудных в данной книжке. Если вы ошалеете от вращений деревьев, попробуйте перейти к следующему разделу о слоёных списках. Прекрасно написанные разделы о красно-черных деревьях вы найдете у Кормена [1990]
Красно-черное дерево - это бинарное дерево с следующими свойствами:
Каждый узел покрашен либо в черный, либо в красный цвет.
Листьями объявляются NIL-узлы (т.е. "виртуальные" узлы, наследники узлов, которые обычно называют листьями; на них "указывают" NULL указатели). Листья покрашены в черный цвет.
Если узел красный, то оба его потомка черны.
На всех ветвях дерева, ведущих от его корня к листьям, число черных узлов одинаково.
Количество черных узлов на ветви от корня до листа называется черной высотой дерева. Перечисленные свойства гарантируют, что самая длинная ветвь от корня к листу не более чем вдвое длиннее любой другой ветви от корня к листу. Чтобы понять, почему это так, рассмотрим дерево с черной высотой 2. Кратчайшее возможное расстояние от корня до листа равно двум - когда оба узла черные. Длиннейшее расстояние от корня до листа равно четырем - узлы при этом покрашены (от корня к листу) так: красный, черный, красный, черный. Сюда нельзя добавить черные узлы, поскольку при этом нарушится свойство 4, из которого вытекает корректность понятия черной высоты. Поскольку согласно свойству 3 у красных узлов непременно черные наследники, в подобной последовательности недопустимы и два красных узла подряд. Таким образом, длиннейший путь, который мы можем сконструировать, состоит из чередования красных и черных узлов, что и приводит нас к удвоенной длине пути, проходящего только через черные узлы. Все операции над деревом должны уметь работать с перечисленными свойствами. В частности, при вставке и удалении эти свойства должны сохраниться.
Чтобы вставить узел, мы сначала ищем в дереве место, куда его следует добавить. Новый узел всегда добавляется как лист, поэтому оба его потомка являются NIL-узлами и предполагаются черными. После вставки красим узел в красный цвет. После этого смотрим на предка и проверяем, не нарушается ли красно-черное свойство. Если необходимо, мы перекрашиваем узел и производим поворот, чтобы сбалансировать дерево.
Вставив красный узел с двумя NIL-потомками, мы сохраняем свойство черной высоты (свойство 4). Однако, при этом может оказаться нарушенным свойство 3, согласно которому оба потомка красного узла обязательно черны. В нашем случае оба потомка нового узла черны по определению (поскольку они являются NIL-узлами), так что рассмотрим ситуацию, когда предок нового узла красный: при этом будет нарушено свойство 3. Достаточно рассмотреть следующие два случая:
Красный предок, красный "дядя": Ситуацию красный-красный иллюстрирует рис. 3.6. У нового узла X предок и "дядя" оказались красными. Простое перекрашивание избавляет нас от красно-красного нарушения. После перекраски нужно проверить "дедушку" нового узла (узел B), поскольку он может оказаться красным. Обратите внимание на распространение влияния красного узла на верхние узлы дерева. В самом конце корень мы красим в черный цвет корень дерева. Если он был красным, то при этом увеличивается черная высота дерева.
Красный предок, черный "дядя": На рис. 3.7 представлен другой вариант красно-красного нарушения - "дядя" нового узла оказался черным. Здесь узлы может понадобиться вращать, чтобы скорректировать поддеревья. В этом месте алгоритм может остановиться из-за отсутствия красно-красных конфликтов и вершина дерева (узел A) окрашивается в черный цвет. Обратите внимание, что если узел X был в начале правым потомком, то первым применяется левое вращение, которое делает этот узел левым потомком.
Каждая корректировка, производимая при вставке узла, заставляет нас подняться в дереве на один шаг. В этом случае до остановки алгоритма будет сделано 1 вращение (2, если узел был правым потомком). Метод удаления аналогичен.
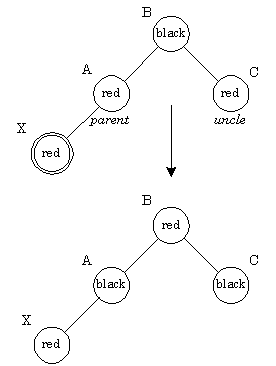
Рис. 3.6. Вставка - Красный предок, красный "дядя"
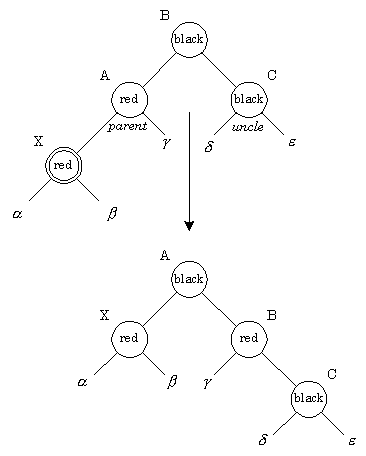
Рис. 3.7. Вставка - красный предок, черный "дядя"




