Лекция 15

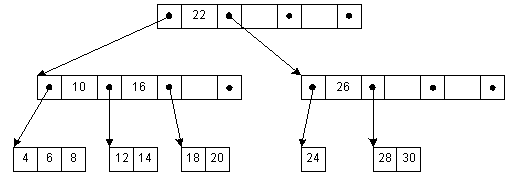
Рис. 4-3. Б-дерево

В этом двухуровневом дереве мы можем добраться до любого ключа за три доступа к диску. Если бы мы сгруппировали по 100 ключей на узел, то за три доступа к диску мы могли бы найти любой ключ из 1000000. Чтобы сохранить это свойство, нам нужно сохранять сбалансированность дерево во время вставок и удалений. Во время вставки мы исследуем потомка, чтобы определить, можно ли добавить в него узел. Если нет, в дерево добавляется еще один брат, а ключи потомка перераспределяются так, чтобы появилось место для нового узла. Когда мы спускаемся, чтобы вставить ключ, и узел оказывается заполненным, мы рассыпаем корень, у которого появляются новые потомки, так что глубина дерева увеличивается. Аналогичные действия предпринимаются при удалении - здесь может потребоваться объединить потомков. Этот метод изменения глубины дерева позволяет сохранить сбалансированность дерева.

 

Таблица 4-1. Реализация Б-деревьев

 

 

В таблице 4-1 приведены несколько вариантов Б-деревьев. В стандартных Б-деревьях ключи и данные хранятся как во внутренних узлах, так и в листьях (концевых узлах). Если при спуске по дереву во время вставки встречен заполненный узел, его содержимое перераспределяется между братьями. Если братья тоже полны, создается новый узел и половина ключей потомка пересылается в него. Во время удаления наполовину заполненные потомки являются первыми кандидатами на добавление ключей из прилежащих узлов. Если сами прилежащие узлы полны лишь наполовину, они объединяются так, чтобы получился полный узел. Б*-деревья устроены аналогично, единственное отличие - узлы заполняются на 2/3. Это приводит к лучшему использованию места, занимаемого деревом, и чуть лучшей производительности.

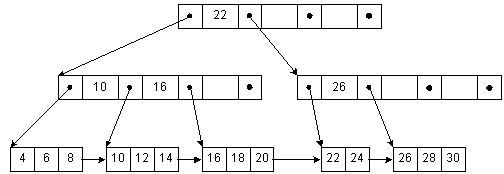
Рис. 4-4. Б⁺-дерево

На рис. 4-4 представлено Б⁺-дерево. Все ключи хранятся в листьях, там же хранится и информационная часть узла. Во внутренних узлах хранятся копии ключей - они помогают искать нужный лист. У указателей смысл немножко не такой, как при работе с обычными Б-деревьями. Левый указатель ведет к ключам, которые меньше заданного значения, правый - ключам, которые больше или равны (GE). Например, к ключам, меньшим 22, ведет левый указатель, а к ключам от 23 и выше ведет правый. Обратите внимание на то, что ключ 22 повторяется в листе, где хранятся соответствующие ему данные. Во время вставки и удаления необходимо аккуратно работать с родительскими узлами. Когда модифицируются первый ключ в листе, дерево проходится от листа к корню. Последний из GE-указателей, найденный при спуске по дереву, и является тем, который потребуется модифицировать, чтобы отразить новое значение ключа. Поскльку все ключи повторяются в листьях, мы можем связать их для последовательного доступа.

Последний метод, Б⁺⁺-деревья, мое изобретение. Оно устроено аналогично Б⁺-деревьям, отличается лишь стратегия расщепления/объединения. Предположим, что в каждом узле могут храниться k ключей, а в корне их может быть 3k. Перед тем, как во время вставки мы спустимся к потому, мы проверяем пуст ли он. Если это так, ключи, находящиеся в потомке и лвух смежных к нему узлах, объединяются и перераспределяются. Если два смежных узла также заполнены, то добавляется узел. Таким образом, мы получаем уже четыре узла, каждый из которых полон на 3/4. Перед тем, как во время удаления спуститься к потомку, мы проверяем, не полон ли он на 1/2. Если это так, ключи потомка и двух смежных узлов объединяются и перераспределяются. Если два смежных узла сами полны наполовину, они сливаются в два узла, каждый из которых полон на 3/4. Мы, таким образом, оказываемся посредине между заполненностью на 1/2 и полной заполненностью, что позволяет нам ожидать равного числа вставок и удалений.

Напомним, что в корневом узле хранятся 3k ключей. Если во время вставки окажется, что корень полон, мы распределяем ключи по четырем новым узлам, каждый из которых полон на 3/4. Это увеличивает высоту дерева. Во время удаления мы исследуем потомков. Если имеется только три потомка и они полны наполовину, переносим их содержимое в корень, в результате чего высота дерева уменьшается.

Другой способ описать работу с деревом - сказать, что мы собираем три узла, а затем рассыпаем их. При вставке, когда нам нужен дополнительный узел, мы рассыпаем на четыре узла. При удалении, когда узел нужно удалить, мы рассыпаем на два узла. Симметрия операций позволяет использовать при реализации вставки и удаления одни и те же собирающие/рассыпающие функции.

Реализация

Среди сопровождающих эти заметки кодах имеется реализация Б⁺⁺-деревьев на ANCI-C. В разделе, зависящем от реализации, необходимо определить bAdrType и eAdrType, которые используются для смещений - в файле Б-дерева и в файле данных соответственно. Вам понадобится также написать функцию, которая используется в алгоритмах Б⁺⁺-дерева для сравнения ключей. Имеются функции, для вставки/удаления ключей, поиска ключей и для последовательного доступа к ключам. Функция main в конце файла - простой пример вставки.

В приведенных кодах допустимы множественные ссылки на одни и те же данные. Реализация использует дескриптор (handle), возвращаемый после открытия индекса. При последующем доступе работа ведется с этим дескриптором. Разрешены повторяющиеся ключи. В пределах одного индекса все ключи должны быть одной длины. Для поиска узлов применяется бираный поиск. Гибкая схема буферизации позволяет удерживать узлы в памяти до тех пор, пока памяти хватает. Если ожидается доступ к чему-нибудь упорядоченному, следует увеличить значение bufCt - это уменьшает число обращений к диску.

 

Исчерпывающий поиск

Поиск с возвращением

Опишем теперь общий метод, позволяющий решить практически любую задачу теории графов и значительно сократить число шагов в алгоритмах типа полного (исчерпывающего) перебора всех возможностей. Чтобы применить этот метод, искомое решение должно иметь вид последовательности áx₁, ..., x_n.ñ Основная идея метода состоит в том, чтобы строить наше решение последовательно, начиная с пустой последовательности (длины 0). Вообще, имея данное частичное решение áx₁, ..., x_iñ, мы стараемся найти такое его допустимое расширение x_i+1; которое либо можно расширить далее, либо оно уже является решением. Если такого расширения не существует, то мы возвращаемся к нашему частичному решению áx₁, ..., x_i-1ñ и продолжаем наш процесс на предыдущем шаге ветвления, отыскивая новое, еще не использованное допустимое значение х'_i. Отсюда название "алгоритм с возвратом” (англ. backtracking).

Точнее говоря, мы предполагаем, что для каждого k > 0 существует некоторое множество A_k, из которого мы будем выбирать кандидатов для k-й координаты частичного решения. Очевидно, что множества A_k должны быть определены для каждого частичного решения áx₁, ..., x_kñ. И если A_k ¹ Æ, то расширение возможно.

Этот алгоритм можно записать в виде следующей схемы:

 

begin k := 1;

    while k > 0 do

      if существует еще неиспользованный элемент y Î A_k  then begin

         х [k] := y; (* элемент y использован *)

         if (x[1],...,x[k]) является решением then write(x[1],...,x[k]);

         k := k + 1

      end

      else (* возврат на более короткое частичное решение; все элементы множества A_k вновь становятся неиспользованными *)

         k := k - 1

end.

 

Покажем также вариант рекурсивного алгоритма поиска с возвратом:

 

procedure BACKTRACK(k);

(*генерирование всех решений, являющихся расширением последовательности x[1],...,x[k-1], массив x -, глобальный *)

begin

  for у Î (A_k \ x) do  begin

    x[k] := у;

    if x[1], ..., x[k] есть решение then

       write (x [1], ..., x [k]);

    BACKTRACK(k + 1)

  end

end.