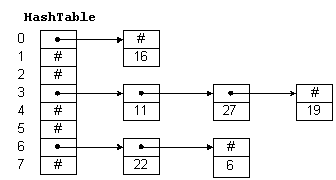
Рис. 3.1. Хеш-таблица

Чтобы вставить в таблицу новый элемент, мы хешируем ключ. Этим мы определяем список, в который его нужно добавить. Затем вставляем элемент в начало этого списка. Например, чтобы добавить 11, мы делим 11 на 8 и получаем остаток 3. Таким образом, 11 следует разместить в списке, на начало которого указывает hashTable[3]. Чтобы найти число, мы его хешируем и проходим по соответствующему списку. Чтобы удалить число, мы находим его и удаляем элемент списка, его содержащий.

При добавлении элементов в хеш-таблицу выделяются куски динамической памяти, которые организуются в виде связанных списков, каждый из которых соответствует входу хеш-таблицы. Этот метод называется связыванием. Другой метод, в котором все элементы располагаются в самой хеш-таблице, известен как прямая или открытая адресация; его описание вы найдете в цитируемой литературе.

Если хеш-функция распределяет совокупность возможных ключей равномерно по множеству индексов, то хеширование эффективно разбивает множество ключей. Наихудший случай - когда все ключи хешируются в один индекс. При этом мы работаем с одним линейным списком, который и вынуждены последовательно сканировать каждый раз, когда что-нибудь делаем. Отсюда видно, как важна хорошая хеш-функция. Здесь мы рассмотрим лишь несколько из возможных подходов. При иллюстрации методов предполагается, что unsigned char располагается в 8 битах, unsigned short int - в 16, unsigned long int - в 32.

Деление (размер таблицы hashTableSize - простое число). Этот метод использован в последнем примере. Хеширующее значение hashValue, изменяющееся от 0 до (hashTableSize - 1), равно остатку от деления ключа на размер хеш-таблицы. Вот как это может выглядеть:

typedef int HashIndexType;

 

HashIndexType Hash(int Key) {

    return Key % HashTableSize;

}

Для успеха этого метода очень важен выбор подходящего значения hashTableSize. Если, например, hashTableSize равняется двум, то для четных ключей хеш-значения будут четными, для нечетных - нечетными. Ясно, что это нежелательно - ведь если все ключи окажутся четными, они попадут в один элемент таблицы. Аналогично, если все ключи окажутся четными, то hashTableSize, равное степени двух, попросту возьмет часть битов Key в качестве индекса. Чтобы получить более случайное распределение ключей, в качестве hashTableSize нужно брать простое число, не слишком близкое к степени двух.

Мультипликативный метод (размер таблицы hashTableSize есть степень 2ⁿ). Значение key умножается на константу, затем от результата берется необходимое число битов. В качестве такой константы Кнут рекомендует золотое сечение (sqrt(5) - 1)/2 = 0.6180339887499. Пусть, например, мы работаем с байтами. Умножив золотое сечение на 28, получаем 158. Перемножим 8-битовый ключ и 158, получаем 16-битовое целое. Для таблицы длиной 25 в качестве хеширующего значения берем 5 младших битов младшего слова, содержащего такое произведение. Вот как можно реализовать этот метод:

/* 8-bit index */

typedef unsigned char HashIndexType;

static const HashIndexType K = 158;

  

/* 16-bit index */

typedef unsigned short int HashIndexType;

static const HashIndexType K = 40503;

  

/* 32-bit index */

typedef unsigned long int HashIndexType;

static const HashIndexType K = 2654435769;

  

/* w=bitwidth(HashIndexType), size of table=2**m */

static const int S = w - m;

HashIndexType HashValue = (HashIndexType)(K * Key)  S;

Пусть, например, размер таблицы hashTableSize равен 1024 (2¹⁰). Тогда нам достаточен 16-битный индекс и S будет присвоено значение 16 - 10 = 6. В итоге получаем:

typedef unsigned short int HashIndexType;

  

HashIndexType Hash(int Key) {

    static const HashIndexType K = 40503;

    static const int S = 6;

    return (HashIndexType)(K * Key)  S;

}

Аддитивный метод для строк переменной длины (размер таблицы равен 256). Для строк переменной длины вполне разумные результаты дает сложение по модулю 256. В этом случае результат hashValue заключен между 0 и 255.

typedef unsigned char HashIndexType;

 

HashIndexType Hash(char *str) {

    HashIndexType h = 0;

    while (*str) h += *str++;

    return h;

}

Исключающее ИЛИ для строк переменной длины (размер таблицы равен 256). Этот метод аналогичен аддитивному, но успешно различает схожие слова и анаграммы (аддитивный метод даст одно значение для XY и YX). Метод, как легко догадаться, заключается в том, что к элементам строки последовательно применяется операция "исключающее или". В нижеследующем алгоритме добавляется случайная компонента, чтобы еще улучшить результат.

typedef unsigned char HashIndexType;

unsigned char Rand8[256];

  

HashIndexType Hash(char *str) {

    unsigned char h = 0;

    while (*str) h = Rand8[h ^ *str++];

    return h;

}

Здесь Rand8 - таблица из 256 восьмибитовых случайных чисел. Их точный порядок не критичен. Корни этого метода лежат в криптографии; он оказался вполне эффективным (Pearson [1990]).

Исключающее ИЛИ для строк переменной длины (размер таблицы <= 65536). Если мы хешируем строку дважды, мы получим хеш-значение для таблицы любой длины до 65536. Когда строка хешируется во второй раз, к первому символу прибавляется 1. Получаемые два 8-битовых числа объединяются в одно 16-битовое.

typedef unsigned short int HashIndexType;

unsigned char Rand8[256];

 

HashIndexType Hash(char *str) {

    HashIndexType h;

    unsigned char h1, h2;

 

    if (*str == 0) return 0;

    h1 = *str; h2 = *str + 1;

    str++;

    while (*str) {

        h1 = Rand8[h1 ^ *str];

        h2 = Rand8[h2 ^ *str];

        str++;

    }

  

    /* h is in range 0..65535 */

    h = ((HashIndexType)h1 << 8)|(HashIndexType)h2;

    /* use division method to scale */

    return h % HashTableSize

}

Размер хеш-таблицы должен быть достаточно большим, чтобы в ней оставалось разумно большое число пустых мест. Как видно из таблицы 3.1, чем меньше таблица, тем больше среднее время поиска ключа в ней. Хеш-таблицу можно рассматривать как совокупность связанных списков. По мере того, как таблица растет, увеличивается количество списков и, соответственно, среднее число узлов в каждом списке уменьшается. Пусть количество элементов равно n. Если размер таблицы равен 1, то таблица вырождается в один список длины n. Если размер таблицы равен 2 и хеширование идеально, то нам придется иметь дело с двумя списками по n/100 элементов в каждом. Это сильно уменьшает длину списка, в котором нужно искать. Как мы видим в таблице 3.1, имеется значительная свободы в выборе длины таблицы.

 

Таблица 3.1. Зависимость среднего времени поиска (µs) от hashTableSize. Сортируются 4096 элементов.