Реализация

В реализации

// Коды для хеш-таблиц

typedef int T;                       /* type of item to be sorted */

#define compEQ(a,b) (a == b)

typedef struct Node_ {

    struct Node_ *next;         /* next node */

    T data;                     /* data stored in node */

} Node;

typedef int hashTableIndex;

Node **hashTable;

int hashTableSize;

hashTableIndex hash(T data) {

   /***********************************

    *  hash function applied to data  *

    ***********************************/

    return (data % hashTableSize);

}

Node *insertNode(T data) {

    Node *p, *p0;

    hashTableIndex bucket;

   /************************************************

    *  allocate node for data and insert in table  *

    ************************************************/

    /* insert node at beginning of list */

    bucket = hash(data);

    if ((p = malloc(sizeof(Node))) == 0) {

        fprintf (stderr, "out of memory (insertNode)\n");

        exit(1);

    }

    p0 = hashTable[bucket];

    hashTable[bucket] = p;

    p->next = p0;

    p->data = data;

    return p;

}

void deleteNode(T data) {

    Node *p0, *p;

    hashTableIndex bucket;

   /********************************************

    *  delete node containing data from table  *

    ********************************************/

    /* find node */

    p0 = 0;

    bucket = hash(data);

    p = hashTable[bucket];

    while (p && !compEQ(p->data, data)) {

        p0 = p;

        p = p->next;

    }

    if (!p) return;

    /* p designates node to delete, remove it from list */

    if (p0)

        /* not first node, p0 points to previous node */

        p0->next = p->next;

    else

        /* first node on chain */

        hashTable[bucket] = p->next;

    free (p);

}

Node *findNode (T data) {

    Node *p;

   /*******************************

    *  find node containing data  *

    *******************************/

    p = hashTable[hash(data)];

    while (p && !compEQ(p->data, data))

        p = p->next;

    return p;

}

Поиск в бинарных деревьях

В разделе 1 мы использовали двоичный поиск

Теория

Двоичное дерево - это дерево, у которого каждый узел имеет не более двух наследников. Пример бинарного дерева приведен на рис. 3.2. Предполагая, что k содержит значение, хранимое в данном узле, мы можем сказать, что бинарное дерево обладает следующим свойством: у всех узлов, расположенных слева от данного узла, значение соответствующего поля меньше, чем k, у всех узлов, расположенных справа от него, - больше. Вершину дерева называют его корнем, узлы, у которых отсутствуют оба наследника, называются листьями. Корень дерева на рис. 3.2 содержит 20, а листья - 4, 16, 37 и 43. Высота дерева - это длина наидлиннейшего из путей от корня к листьям. В нашем примере высота дерева равна 2.

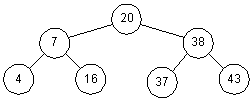
Рис. 3.2. Двоичное дерево

Чтобы найти в дереве какое-то значение, мы стартуем из корня и движемся вниз. Например, для поиска числа 16, мы замечаем, что 16 < 20, и потому идем влево. При втором сравнении видим, что 16 > 7, и потому мы движемся вправо. Третья попытка успешна - мы находим элемент с ключом, равным 16.

Каждое сравнение вдвое уменьшает количество оставшихся элементов. В этом отношении алгоритм похож на двоичный поиск в массиве. Однако, все это верно только в случаях, когда наше дерево сбалансировано. На рис. 3.3 показано другое дерево, содержащее те же элементы. Несмотря на то, что это дерево тоже бинарное, поиск в нем похож, скорее, на поиск в односвязном списке, время поиска увеличивается пропорционально числу запоминаемых элементов.

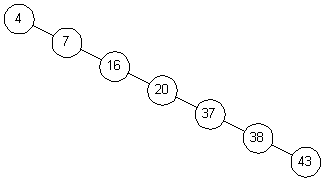
Рис. 3.3. Несбалансированное бинарное дерево

Вставка и удаление

Чтобы лучше понять, как дерево становится несбалансированным, посмотрим на процесс вставки пристальнее. Чтобы вставить 18 в дерево на рис. 3.2 мы сначала должны найти это число. Поиск приводит нас в узел 16, где благополучно завершается. Поскольку 18 16, мы попросту добавляет узел 18 в качестве правого потомка узла 16 (рис. 3.4).

На этом примере хорошо видно, как возникает несбалансированность дерева. Если данные поступают в возрастающем порядке, каждый новый узел добавляется справа от последнего вставленного. Это приводит к одному длинному списку. Обратите внимание: чем более "случайны" поступающие данные, тем более сбалансированным получается дерево.

Удаления производятся примерно так же - необходимо только позаботиться о сохранении структуры дерева. Например, если из дерева на рис. 3.4 удаляется узел 20, его сначала нужно заменить на узел 37. Это даст дерево, изображенное на рис. 3.5. Рассуждения здесь примерно следующие. Нам нужно найти потомка узла 20, справа от которого расположены узлы с большими значениями. Таким образом, нам нужно выбрать узел с наименьшим значением, расположенный справа от узла 20. Чтобы найти его, нам и нужно сначала спуститься на шаг вправо (попадаем в узел 38), а затем на шаг влево (узел 37); эти двухшаговые спуски продолжаются, пока мы не придем в концевой узел, лист дерева.

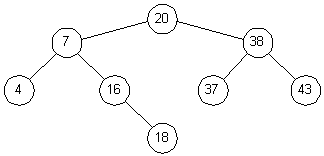
Рис. 3.4. Бинарное дерево после добавления узла 18

 

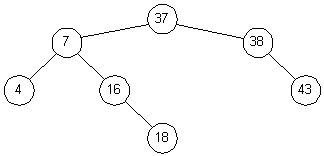
Рис. 3.5. Бинарное дерево после удаления узла 20